Simulation von unabhängigen Universen zum Studium der Strukturbildung in der dunklen Materie
Im kosmologischen Standardmodell macht die dunkle Materie etwa 25% des gesamten Energiebudgets des Universums aus. Sie kann aber nicht direkt beobachtet werden, da sie kein Licht emittiert. Dabei ist das Verständnis der Art und Weise, wie dunkle Materie Strukturen formt und Haufen bildet, von entscheidender Bedeutung. Es trägt nicht nur zu unserem Verständnis der beobachteten räumlichen Verteilung der Galaxien bei (die der Verteilung der dunklen Materie folgt), sondern erlaubt uns Rückschlüsse auf die winzigen anfänglichen Dichtefluktuationen im frühen Universum, aus denen sich die Struktur gebildet hat. In diesem Zusammenhang haben Forscher am MPA und anderen Institutionen weltweit eine neue Art von Simulationen entwickelt, die sogenannten Simulationen von "unabhängigen Universen", um die Auswirkungen von großskaligen (oder langwelligen) Dichtefluktuationen auf die Strukturen zu untersuchen, die zu späten Zeiten beobachtet werden. Mit dieser Technik haben die MPA-Forscher vor kurzem einige der präzisesten Messungen des sogenannten lokalen Bias erzielt, welche den bereits bekannten Trend bestätigen, dass massereichere Halos einem stärkeren Bias unterliegen als kleinere Halos.
Strukturbildung der dunklen Materie
Unter dem Einfluss der Schwerkraft häuft sich Dunkle Materie in verschieden großen Strukturen an und bildet damit das sogenannte kosmische Netz (siehe Abbildung 1). Eine der wichtigsten Komponenten dabei sind die sogenannten Halos, d.h. Regionen, in denen sich dunkle Materie angesammelt hat. Die Menge und Verteilung dieser Halos hängt stark von der Verteilung der dunklen Materie ab, oder anders gesagt: die Halo-Verteilung unterliegt einem Bias in Bezug auf die Verteilung der dunklen Materie. Diesen Bias zu verstehen und welche physikalischen Effekte ihn beeinflussen, ist von entscheidender Bedeutung für die statistische Beschreibung der Halo-Verteilung. Dies wiederum ist sehr wichtig, da nach dem kosmologischend Standardmodell sichtbare kosmische Objekte (wie Galaxien oder Galaxienhaufen) vorzugsweise in Halos aus dunkler Materie liegen. Dies wurde auch mit dem Gravitationslinseneffekt bereits direkt nachgewiesen.
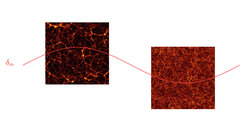
Um die Anhäufung der dunklen Materie zu untersuchen, führen Physiker traditionell so genannte "N-Körper"-Simulationen durch. In ihrer einfachsten Form verfolgen diese Simulationen die Entwicklung einer gewissen Anzahl an Teilchen in einem würfelförmigen Volumen ("Box") unter dem Einfluss der Schwerkraft von einer anfänglichen, fast homogenen Verteilung bis zu einem späteren Zeitpunkt. Dabei steht der Begriff "Teilchen" für "Massenelement"; diese Teilchen können typischerweise einige Millionen oder sogar Milliarden Sonnenmassen groß sein, da wir nicht in der Lage sind, eine unendliche Massenauflösung zu erreichen. Um eine möglichst breite Skala abzudecken, müssen diese Simulationen sowohl eine große Anzahl von Teilchen (einige Milliarden) umfassen als auch ein größtmögliches Volumen haben (bis zu einigen Gpc pro Seite); dies macht sie schnell zu rechnerisch kostspieligen Anwendungen.
Simulationen von unabhängigen Universen
Die Grundidee hinter den Simulationen von unabhängigen Universen ist, dass ein Teilbereich des Universums, der eine andere Materiedichte hat, als ein separates Universum behandelt wird. Man kann zeigen, dass eine homogene Veränderung der Materiedichte in einer Simulation (d.h. eine Störung mit einer unendlichen Wellenlänge) gleichbedeutend ist damit, die Simulation mit unterschiedlichen kosmologischen Parametern durchzuführen (z. B. eine gekrümmte statt einer flachen Geometrie). Es ist somit möglich, eine kostspielige große Simulation in mehrere kleinere zu unterteilen, wobei jede eine andere Materiedichte hat und die kosmologischen Parameter korrekt angepasst werden müssen. Somit kann die Abhängigkeit, beispielsweise, der Halo-Dichte von der Materiedichte mathematisch sauber untersucht werden.
Diese Technik macht nicht nur die Durchführung von Simulationen einfacher, sie ermöglicht es außerdem, die Auswirkungen von großflächigen Dichtefluktuationen auf kleinere Skalen zu messen, auf denen Halo- und Galaxienbildung stattfindet. Da die langwellige Dichtefluktuation nunmehr ein Parameter ist, der unabhängig gewählt werden kann, ist es möglich, die Abhängigkeit der Strukturbildung allein von diesem Parameter zu messen - anders als bei herkömmlichen N-Körpersimulationen, bei denen ein Vermischen der Skalen unvermeidbar ist. Daher bietet dieses Verfahren eine schnelle und einfache Möglichkeit, genaue Messungen von Größen in Abhängigkeit der Materiedichte zu machen.
Ein Maß für die Strukturbildung: Halo-Bias
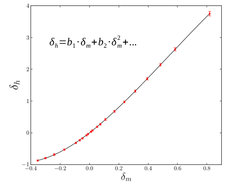
Abbildung 2: Die Abhängigkeit der Halo-Dichte (δh) von der Materiedichte (δm) in unabhängigen Universen. Rote Punkte sind die Ergebnisse der Simulationen, die schwarze Linie zeigt ein an die Messungen angepasstes Polynom, dessen Koeffizienten genau die lokalen Bias-Parameter sind.
Eine solche Größe ist die Anzahl der in einer Simulation gefundenen dunklen Materie-Halos. Wie oben erwähnt, ist der Bias eine statistische Größe, der die Halo-Anzahl (in einem vorgegebenen Volumen) mit der Materiedichte verbindet. Es gibt viele verschiedene Bias-Parameter, die die verschiedenen physikalischen Effekte darstellen, die in die Strukturbildung eingehen. Der meist untersuchte Bias-Parameter auf großen Skalen ist der sogenannte lokale Bias. Dieser Parameter beschreibt das Verhältnis der Halo-Dichte zur Materiedichte an jedem Ort in der Simulation.
Die Simulation von unabhängigen Universen bietet einen perfekten Rahmen, um präzise Messungen dieser Größe zu erhalten, da man einfach mehrere Simulationen mit verschiedenen Werten für die Materiedichte durchführen kann und dann nur die Anzahl der resultierenden dunklen Materie-Halos in jeder Simulation messen muss. Die so gewonnene Beziehung zwischen Materie- und Halo-Dichte gibt dann den lokalen Bias als Proportionalitätskonstante zwischen diesen beiden Größen (siehe Abb. 2).
Offensichtlich führen Simulationen mit einer höheren Anfangsdichte später zu einer höheren Halo-Dichte, wie auch in Abbildung 1 zu sehen ist. Mit dieser Technik erzielten die MPA-Forscher vor kurzem einige der präzisesten Messungen des lokalen Bias und bestätigten den bekannten Trend, dass massereichere Halos (die gleichzeitig weniger häufig sind) einem größeren Bias unterliegen als kleinere Halos.













