Gravitational Radiation from General Relativistic Rotational Core Collapse
H. Dimmelmeier, J.A. Font, E. Müller
Introduction:
Whereas light or sound waves propagate through spacetime, gravitational waves are propagating ripples of spacetime itself. Such distortions in spacetime, which can for example be measured by laser interferometric detectors, are generated by aspherical concentrations of moving matter. However, as this effect is so small, even the most violent astrophysical phenomena involving extremely compact objects (like, e.g., colliding and merging black holes or neutron stars, or collapsing stars) emit gravitational waves which, given the typical distance to the event, manifest themselves as a tiny relative effect of only 10-20 on Earth.
Not surprisingly, although gravitational waves have been predicted by Albert Einstein in his theory of general relativity over 80 years ago, only now technology enables physicists to tackle the problem of detecting them. A successful direct detection of gravitational waves, which can be envisaged within the next 5 years, will not only unequivocally prove Einstein's bold prediction (which today is not seriously doubted anymore), but even more interestingly, will open a completely new "window" onto the universe. By routinely observing gravitational waves, astrophysicists will gain new and otherwise entirely unattainable insights into such fascinating objects like black holes, the enigmatic cosmic gamma ray bursts, or the driving engines behind stellar supernova explosions [Thorne, 1997].
In order to accomplish a successful detection of gravitational waves, very efficient electronic filters have to be employed to extract a possible signal from the data measured by a detector [Arnaud, et al., 1998], which make use of the typical form of a prospective gravitational wave signal. It is therefore of great importance to predict as precise as possible the signals from theoretical models (so called wave templates) of various astrophysical sources of gravitational radiation. Moreover, by comparing the predicted signals with those actually detected, astrophysicists can test and constrain their models and eventually gain a better understanding of the fundamental physical processes which govern the event.
One example of a promising source of gravitational waves is the gravitational collapse of the rapidly rotating core of a massive star to a neutron star and the subsequent explosion of the star as a supernova. The gravitational wave signals produced typically consist of a strong short burst with a complicated temporal structure, and they depend crucially on many aspects of the complicated physics involved in this powerful event.
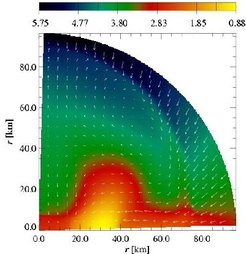
Extending previous simulations [Zwerger and Müller, 1997], we have succeeded for the first time to simulate the collapse of a rotating stellar core to a neutron star including the effects of general relativity [Dimmelmeier, et al., 2001, Dimmelmeier, et al., 2002a, Dimmelmeier, et al., 2002b], making a major step towards realistic predictions of gravitational wave signals. The results of these new simulations show that improvements in the physical model underlying the numerical simulation - though a priori considered to be of rather modest size - can have a huge impact on the gravitational wave signal.
These new simulations will help observers to identify and extract gravitational wave signals in their future measurements. Furthermore, they also allow to draw conclusions about the circumstances of the actual supernova event from a possible signal, extending far beyond the knowledge we can obtain from observations of the emitted light with conventional optical telescopes.
Simulations:
In the following, we summarize the assumptions and approximations of our core collapse simulations. For more details, we refer to [Dimmelmeier, et al., 2002a, Dimmelmeier, et al., 2002b].
We have simulated a set of 26 rotational supernova core collapse models in axisymmetry. To simulate these models, we numerically solve the fully general relativistic hydrodynamic equations in a flux-conservative formulation [Banyuls, et al., 1997] on a grid using spherical coordinates. For an accurate resolution of shocks, we have implemented a modern high-resolution shock-capturing scheme, which uses characteristic information of relativistic hydrodynamics [Font, 2000]. The exact metric in the ADM spacetime foliation is approximated by assuming conformal flatness for the three-metric (also known as conformal flatness condition (CFC) or Isenberg-Wilson-Mathews approximation [Wilson, et al., 1996]), which significantly reduces the complexity of the hydrodynamic and metric equations.
The initial configurations are rotating 4/3-polytropes in equilibrium with a central density of ρc ini = 1010 g/cm3 constructed by numerically solving the hydrodynamic equilibrium equations in a general relativistic spacetime [Komatsu, et al., 1989a, Komatsu, et al., 1989b]. The initial state is completely determined by the central density, the rotation rate βrot ini = Erot ini / Epot ini, and the rotation parameter A, which specifies the degree of differential rotation.
The equation of state during core collapse consists of a polytropic and a thermal contribution. The collapse is initiated by reducing the adiabatic exponent γ1. For densities ρ > 2.0 . 1014 g/cm3, the adiabatic exponent is set to γ1 = 2.5 mimicking the stiffening of the equation of state above nuclear matter density. We have also simulated one model with a soft supranuclear equation of state with γ1 = 2.0.
A summary of important quantities for all 26 models simulated in relativistic and Newtonian gravity is available in an HTML table or a gzipped PS table. The name of a model is determined by the value of the three free parameters according to the following table:
The collapse dynamics can be viewed in a series of movies of four representative core collapse models.
We provide a waveform catalog of all simulated models. Additionally, you can click on the following shortcuts to view figures of the waveforms in various formats or download raw data of the waveforms.
Figures of the waveforms in EPS format
Figures of the waveforms in JPG format
Gravitational wave signal data
(gzipped tar archive, 21 MByte, including a README file).
Density evolution data
(gzipped tar archive, 15 MByte, including a README file).
Gravitational wave energy data
(gzipped tar archive, 20 MByte, including a README file).
Presentations:
A more detailed overview about this project, the results, and the background of the current applications in astrophysical simulations can be found in two color slide presentations:
Overview presentation in PDF format (1.0 MB).
Technical presentation in PDF format (1.5 MB).
References:
- Arnaud, N., Davier, M., Cavalier, F., and Hello, P.,
"Detection of gravitational wave bursts by interferometric detectors",
Phys. Rev. D, 59, 082002, (1999),
[Article in gr-qc].
- Banyuls, F., Font, J.A., Ibanez, J.M., Marti, J.M., Miralles, J.A.,
"Numerical {3+1} general relativistic hydrodynamics",
Astrophys. J., 476, 221-231, (1997),
[Article in PDF format via Astrophys. J.].
- Dimmelmeier, H., Font, J.A., and Müller, E.,
"Gravitational waves from relativistic rotational core collapse",
Astrophys. J. Lett., 560, L163-L166, (2001),
[Article in astro-ph].
- Dimmelmeier, H., Font, J.A., and Müller, E.,
"Relativistic simulations of rotational core collapse. I. Methods, initial models, and code tests",
Astron. Astrophys., 388, 917-935, (2002),
[Article in astro-ph].
- Dimmelmeier, H., Font, J.A., and Müller, E.,
"Relativistic simulations of rotational core collapse. II. Collapse dynamics and gravitational radiation",
Astron. Astrophys., 393, 523-542, (2002),
[Article in astro-ph].
- Font, J.A.,
"Numerical hydrodynamics in general relativity",
Living Rev. Relativ., 3, (2000),
[Article in Living Rev. Relativ.].
- Komatsu, H., Eriguchi, Y., and Hachisu, I.,
"Rapidly rotating general relativistic stars - I. Numerical method and its application to uniformly rotating polytropes",
Mon. Not. R. Astron. Soc., 237, 355-379, (1989),
[Article in PDF format via ADS].
- Komatsu, H., Eriguchi, Y., and Hachisu, I.,
"Rapidly rotating general relativistic stars - II. Differentially rotating polytropes",
Mon. Not. R. Astron. Soc., 239, 153-171, (1989)
[Article in PDF format via ADS].
- Thorne, K.S.,
"Probing black holes and relativistic stars with gravitational waves", (1997),
[Article in gr-qc].
- Wilson, J.R., Mathews, G.J., and Marronetti, P.,
"Relativistic numerical model for close neutron-star binaries",
Phys. Rev. D, 54, 1317-1331, (1996),
[Article in gr-qc].
- Zwerger, T., and Müller, E.,
"Dynamics and gravitational wave signature of axisymmetric rotational core collapse",
Astron. Astrophys., 320, 209-227, (1997),
[Article in PDF format via ADS].