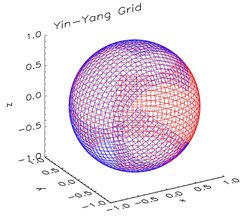
Yin-Yang grid
A.Wongwathanarat, N.J.Hammer, and Ewald Müller
Three dimensional explicit hydrodynamic codes based on spherical polar coordinates using a single spherical polar grid suffer from a severe restriction of the time step size due to the convergence of grid lines near the poles of the coordinate system, and from numerical artifacts at the symmetry axis of the grid. The first problem can be eased and the second one avoided by applying an overlapping grid technique called Yin-Yang grid, which is a two-patch overset grid proposed by Kageyama & Sato (2004) for geophysical simulations.
The Yin-Yang grid consists of two overlapping grid patches named "Yin" and "Yang" grid. In comparison with other types of overset grids in spherical geometry, the Yin-Yang grid geometry is simple, as both the Yin and the Yang grid consist of a part of a usual spherical polar grid. The transformation of coordinates and vector components between the two patches is straightforward and symmetric, thus allowing for an easy and straightforward implementation of the grid into a 3D code already employing spherical polar coordinates.
The Yin-Yang grid has been implemented by us (Wongwathanarat et. al, 2010) into the explicit Eulerian grid-based finite volume hydrodynamics code PROMETHEUS including self-gravity. The modified code successfully has passed several standard hydrodynamic tests producing results which are in very good agreement with analytic solutions. Moreover, the solutions obtained with the Yin-Yang grid exhibit no peculiar behaviour at the boundary between the two grid patches.
The code has also been successfully applied to simulations of core collapse supernovae (Wongwathanarat et. al, 2013, 2015). According to our results, the usage of the Yin-Yang grid greatly enhances the suitability and efficiency of 3D explicit Eulerian codes based on spherical polar coordinates for astrophysical flows.
References:
Wongwathanarat, A., Müller, E. and Janka, H.-T., Three-dimensional simulations of core-collapse supernovae: from shock revival to shock breakout, AAP, 2015, 577.
Wongwathanarat, A., Janka, H.-T. and Müller, E., Three-dimensional neutrino-driven supernovae: Neutron star kicks, spins, and asymmetric ejection of nucleosynthesis products, AAP, 2013, 552.
Wongwathanarat, A., Hammer, N J. and Müller, E., An axis-free overset grid in spherical polar coordinates for simulating 3D self-gravitating flows, AAP, 2010, 514.
Kageyama, A. and Sato, T., "Yin-Yang grid"': An overset grid in spherical geometry, Geochemistry Geophysics Geosystems, 2004, Vol 5, Number 9.
