Simulations of Rotational Stellar Core Collapse in General Relativity with Microphysics (Extended Model Set)
H. Dimmelmeier, C.D. Ott, A. Marek, H.-T. Janka
Simulations:
We have simulated a set of 136 rotational supernova core collapse models in axisymmetry. To simulate these models, we numerically solve the fully general relativistic hydrodynamic equations in a flux-conservative formulation [Banyuls, et al., 1997] on a grid using spherical coordinates. For an accurate resolution of shocks, we have implemented a modern high-resolution shock-capturing scheme, which uses characteristic information of relativistic hydrodynamics [Font, 2000]. The exact metric in the ADM spacetime foliation is approximated by assuming conformal flatness for the three-metric, which significantly reduces the complexity of the hydrodynamic and metric equations.
As initial configuration we choose the presupernova stellar models e15a, e15b, e20a, e20b, s11.2, s15, s20, or s40 [Woosley, et al., 2002]. The progenitor models e15a, e15b, e20a, and e20b have an angular momentum distribution from stellar evolution calculations, while on the s11.2, s15, s20, and s40 models we impose rotation [Komatsu, et al., 1989a, Komatsu, et al., 1989b] with different rates and profiles.
During core collapse, we utilize a microphysical equations of state specifically designed for supernova core collapse, either the one by Shen et al. (Shen EoS) [Shen, et al., 1998] or the one by Lattimer and Swesty (LS EoS) [Lattimer and Swesty, 1998]. To approximate the effects of neutrinos in the infall phase, a very efficient parametric deleptonization scheme is used [Liebendörfer, 2005].
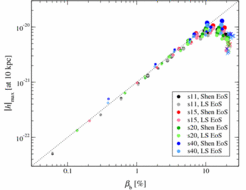
Again, as for previous models with a more restricted selection of free parameters, we find that the gravitational wave burst signal from core bounce is very uniform. We also observe the effects of the centrifugal barrier on the collapse dynamics for rapidly rotating models, which effectively prevents the collapsing core from reaching the very high rotation rates needed for becoming unstable to dynamical rotation instabilities. This mechanism also limits the amplitude of the waveform for gravitational radiation.
A detailed description of the models and other interesting information can be found in a published article [Dimmelmeier, et al., 2008].
We provide a waveform catalog of all simulated models. Additionally, you can click on the following shortcuts to view figures of the waveforms in various formats or download raw data of the waveforms.
Figures of the waveforms in EPS format
Figures of the waveforms in JPG format
Gravitational wave signal data
(gzipped tar archive, 9.8 MByte, including a README file).
Density evolution data
(gzipped tar archive, 6.3 MByte, including a README file).
References:
- Dimmelmeier, H., Font, J.A., and Müller, E.,
"Gravitational waves from relativistic rotational core collapse",
Astrophys. J. Lett., 560, L163-L166, (2001),
[Article in astro-ph].
- Dimmelmeier, H., Font, J.A., and Müller, E.,
"Relativistic simulations of rotational core collapse. I. Methods, initial models, and code tests",
Astron. Astrophys., 388, 917-935, (2002),
[Article in astro-ph].
- Dimmelmeier, H., Font, J.A., and Müller, E.,
"Relativistic simulations of rotational core collapse. II. Collapse dynamics and gravitational radiation",
Astron. Astrophys., 393, 523-542, (2002),
[Article in astro-ph].
- Dimmelmeier, H., Ott, C.D., Janka, H.-T., Marek, A., and Müller, E.,
"Generic gravitational wave signals from the collapse of rotating stellar cores",
Phys. Rev. Lett., 98, 251101, (2007),
[Article in astro-ph].
- Dimmelmeier, H., Ott, C.D., Marek, A., and Janka, H.-T.,
"The gravitational wave burst signal from core collapse of rotating stars",
Phys. Rev. D, 78, 064056, (2008),
[Article in astro-ph].
- Komatsu, H., Eriguchi, Y., and Hachisu, I.,
"Rapidly rotating general relativistic stars - I. Numerical method and its application to uniformly rotating polytropes",
Mon. Not. R. Astron. Soc., 237, 355-379, (1989),
[Article in PDF format via ADS].
- Komatsu, H., Eriguchi, Y., and Hachisu, I.,
"Rapidly rotating general relativistic stars - II. Differentially rotating polytropes",
Mon. Not. R. Astron. Soc., 239, 153-171, (1989)
[Article in PDF format via ADS].
- Liebendörfer, M.,
"A simple parameterization of the consequences of deleptonization for simulations of stellar core collapse",
Astrophys. J., 633, 1042-1051, (2005)
[Article in astro-ph].
- Ott, C.D., Dimmelmeier, H., Marek, A., Janka, H.-T., Hawke, I., Zink, B., and Schnetter, E.,
"3D collapse of rotating stellar iron cores in general relativity with microphysics",
Phys. Rev. Lett., 98, 261101, (2007),
[Article in astro-ph].
- Ott, C.D., Dimmelmeier, H., Marek, A., Janka, H.-T., Zink, B., Hawke, I., and Schnetter, E.,
"Rotating collapse of stellar iron cores in general relativity",
Class. Quantum Grav., 24, S139-S154, (2007),
[Article in astro-ph].
- Shen, H., Toki, H., Oyamatsu, K., and Sumiyoshi, K.,
"Relativistic Equation of State of Nuclear Matter for Supernova Explosion",
Prog. Theor. Phys., 100, 1013-1031, (1998)
[Article in PDF format via Prog. Theor. Phys.].
- Woosley, S.A, Heger, A., and Weaver, T.A.,
"The evolution and explosion of massive stars",
Rev. Mod. Phys., 74, 1015-1071, (2002)
[Article in PDF format via Rev. Mod. Phys.].
